报告题目1：SINGULAR INTEGRAL ASSOCIATED WITH ZYGMUND DILATIONS

报告人：韩永生教授，美国Auburn大学

报告时间：2023年12月25日（周一）14:30

报告地点：20-306

报告摘要：The multiparameter theory of R^n began with Zygmund’s study of the strong maximal function and then continued with Marcinkiewicz’s proof of his multiplier theorem. Jensen–Marcinkiewicz–Zygmund proved that the strong maximal function in R^n is bounded from the Orlicz space L(1+ (log^{+}L)^{n−1}) to weak L^{1}. Zygmund further conjectured that if the rectangles in Rn had n side lengths which involve only k independent variables, then the resulting maximal operator should behave like Mk, the k-parameter strong maximal operator. Cordoba showed that Llog^{+}L to weak L^{1} for the maximal function on R^{3} defined by

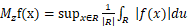
The supremum above is taken over all rectangles with sides parallel to the axes and side lengths of the form s, t, and st. Stein was the first to link the properties of maximal operators associated with Zygmund dilations to boundary value problems for Poisson integrals on symmetric spaces, such as Siegel’s upper half space.

In this talk, we consider the boundedness for singular integrals associated with the Zygmund dilations.

报告人简介：韩永生教授1981年于北京大学获得硕士学位，1984年在美国Washington University大学师从鼎鼎大名的调和分析大师G. Weiss 教授，获得博士学位。目前，他是美国Auburn大学数学系终身教授。韩永生教授长期从事调和分析的教学与研究，尤其是函数空间理论，已在国内外期刊 Trans. Amer. Math. Soc., Forum Math., Ann. Scuola Norm. Sup. Pisa Cl. Sci., J. Geometric Analysis, Journal of Functional Analysis,  Revista Mathematica Iberoamericana, Analysis and PDE, Mem. Amer. Math. Soc., Math. Z.等杂志发表学术论文。撰写出版专著《Harmonic Analysis on Spaces of Homogeneous Type》，《Hp空间》，《近代调和分析方法及其应用》。

报告题目2：T1 theorem and Tb theorem on Lipschitz space, Besov and Triebel-Lizorkin space

报告人：郑涛涛副教授，浙江科技大学

报告时间：2023年12月25日（周一）15:40

报告地点：20-306

报告摘要：This talk contains two parts, for one-parameter case, we introduce the T1 theorem and the Tb theorem on Lipschitz space, Besov and Triebel-Lizorkin space. For multi-parameter case, we study the boundedness of product Calder\'{o}n-Zygmund  operator on product Lipschitz space, product weighted Besov and Triebel-Lizorkin space and the dual of product weighted Hardy space.

报告人简介：郑涛涛，浙江科技大学副教授、硕士生导师，2015年毕业于浙江大学数学系，获理学博士学位，2018.09-2019.09 美国奥本大学访问学者。主要从事调和分析及其应用等方面的研究工作。第二批浙江省高校“双带头人”教师党支部书记工作室负责人，先后主持国家自然科学基金与浙江省自然科学基金各1项，参与国家自然科学基金4项。在 J. Geom. Anal.、New York J. Math.、Banach J. Math. Anal.、中国科学：数学等期刊上发表论文20余篇。