报告题目1：A new proof for the regularity of Monge-Ampere type equations

报告人1：吴雅婷博士，华中师范大学

报告时间：2023年12月6日（周三）18:30-19:30

报告地点：腾讯会议：631-435-693

报告摘要：In this talk, we will discuss the interior 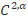 regularity for Monge-Ampere type equations. Our proof uses the Green function for linear elliptic equations. The proof is elementary, it uses only the Green function and some well known techniques in analysis. This is a joint work with Xu-Jia Wang.

个人简介：吴雅婷，博士，2022年毕业于澳大利亚伍伦贡大学。主要的研究方向为完全非线性椭圆型偏微分方程，尤其是Monge-Ampère方程和k-Hessian方程解的正则性问题，研究成果发表于 Journal of Differential Geometry，Indiana University Mathematics Journal。目前获得2023年度国家自然科学青年基金，第73批博士后面上项目，2023年度湖北省博士后创新研究岗位。

报告题目2：Spiraling solutions to the nonlinear stationary Schr\"odinger equation

报告人2：帅伟副教授，华中师范大学

报告时间：2023年12月6日（周三）19:30-20:30

报告地点：腾讯会议：631-435-693

报告摘要：In this paper, we investigate sign-changing partially localized solutions to the following nonlinear elliptic equation

\begin{equation*}

-\Delta v -v_{yy}+q v= |v|^{p-2}v, \ \ (x,y)\in {\R}^N\times{\R},

\end{equation*}

where $N\geq 2$, $q\in {\R}$ and $p\in (2,2^*)$. Our main focus is on the existence of sign-changing partially localized solutions that exhibit periodicity in $y$. These solutions are bounded and possess a spiraling behavior, meaning that they are not axially symmetric but remain invariant under screw motion, resembling the symmetry properties of a helicoid.

个人简介：帅伟，理学博士，华中师范大学副教授。2016年博士毕业于华中师范大学，师从邓引斌教授。2016.12-2018.12 香港中文大学数学科学研究所，助理研究员，合作导师为辛周平教授。主要研究方向是非线性椭圆型偏微分方程、非线性泛函分析。主要成果发表在J. Funct. Anal., Calc. Var. Partial Differential Equations, J. Differential Equations等国际期刊上。现主持国家自然科学基金面上项目一项。

邀请人：杨涛