报告题目1：Bifurcations of Z_q-equivariant vector fields and possible configurations of limit cycles

报告人：李继彬教授，华侨大学

报告时间：2023年10月25日8:00-9:00

报告地点：20-404

报告摘要：Like the first part of Hilbert's 16th problem where the distribution of ovals is to be considered, the distribution problem of limit cycles can also be very interesting. Coleman [1983] in his survey“Hilbert 16th problem: How Many Cycles?” stated that “For n>2 the maximal number of eyes is not known, nor is it known just which complex patterns of eyes within eyes, or eyes enclosing more than a single critical point, can exist.” Here so-called “eye means the limit cycle. In order to obtain more limit cycles and various configuration patterns of their relative dispositions, we indicated that an efficient method is to perturb the symmetric Hamiltonian systems having maximal number of centers, i.e. to study the weakened Hilbert's 16th problem for the symmetric planar polynomial Hamiltonian systems, since bifurcation and symmetry are closely connected and symmetric systems play pivotal roles as a bifurcation point in all planar Hamiltonian system class. To investigate perturbed Hamiltonian systems, we should first know the global behavior of unperturbed polynomial systems, namely, determine the global property for the families of real planar algebraic curves defined by the Hamiltonian functions. Then by using proper perturbation techniques, we shall obtain the global information of bifurcations for the perturbed nonintegrable systems.

In this talk, we introduce the method of detection functions posed by Li et al. [1985], to study the Z_q-equivariant perturbed polynomial systems and the method of control parameters. We also present recent developments in this direction.

报告人简介：李继彬，华侨大学和浙江师范大学特聘教授，博士生导师，动力系统与非线性研究中心负责人。曾任四届国家自然科学基金委数学学科评审专家组成员，云南省科学技术委员会常务委员，三届云南省数学会理事长，云南省应用数学研究所副所长，昆明理工大学理学院院长等。现为《应用数学与力学》等全国和国际性刊物的编委；美国《数学评论》与德国《数学文摘》评论员。主持承担国家自然科学基金重点项目和面上科研项目等10余项，发表论文230余篇，出版中英文专著10部，主编教材两部、出版科普书两本。三十余年培养硕士和博士研究生70余人。科研成果曾分别获云南省和浙江省科学技术一等奖。1987-2018年，先后三十余次应邀到美国、俄国、法国、加拿大、德国、英国、澳大利亚、西班牙、新加坡、南非等国家和香港、澳门、台湾等地区多所大学和研究机构进行科研合作与学术交流。

报告题目2：Dynamics of iteration operator

报告人：张伟年教授，四川大学

报告时间：2023年10月25日9:00-10:00

报告地点：20-404

报告摘要：The semi-dynamical system of a continuous self-map is generated by iteration of the map, however the iteration itself, being an operator on the space of continuous self-maps, may generate interesting dynamical behaviors. In this talk, we characterize its fixed points and periodic points in the case that the compact metric space is a compact interval and prove that all orbits of the iteration operator are bounded but most fixed points are not stable. On the other hand, we prove that the iteration operator is not chaotic. This is a joint work with Murugan Veerapazham and Chaitanya Gopalakrishna.

报告人简介：张伟年，四川大学教授，数学学院院长，博士生导师。从事微分方程与动力系统的理论研究和应用，包括微分方程形式的连续型动力系统和差分迭代形式的离散动力系统。在国家核心和国际学术期刊上已发表学术论文100余篇，其中SCI收录80余篇，出版专著3部，教材1部，主持国家自然科学基金重点项目等10余项。多次应邀到加拿大滑铁卢大学、英国Warwick大学、法国南特中央大学、Brigham Young大学等国外著名大学开展科研合作。入选四川大学214人才工程、国家985科技创新平台、四川大学教学名师，四川省教学名师，并获得中国青年科技奖等多项奖励和荣誉。

报告题目3：The number of limit cycles near a double homoclinic loop for a non-symmetric near-Hamiltonian system

报告人：杨俊敏教授，河北师范大学

报告时间：2023年10月25日10:00-11:00

报告地点：20-404

报告摘要：In this paper, we give several general conditions on obtaining the number of limit cycles near a double homoclinic loop for a non-symmetric near-Hamiltonian system, and obtain the distributions of limit cycles. For a cubic Hamiltonian system under polynomial perturbations with degree n(3≤n≤20), we obtain a lower bound of the maximum number of limit cycles near a double homoclinic loop.

报告人简介：杨俊敏，河北师范大学教授，博士生导师。2011年1月毕业于上海师范大学，获理学博士学位，博士毕业论文在2013年获得“上海市研究生优秀成果(学位论文)”奖。现主要从事微分方程与动力系统方向的研究工作，主要研究内容为非线性微分系统的分支问题，包括Hopf分支、同宿分支、异宿分支等。在《J. Differential Equations》、《Nonlinear Anal.》、《Discrete Contin. Dyn. Syst.》、《Appl. Math. Comput.》、《J. Dynam. Differential Equations》、《Internat. J. Bifur. Chaos Appl. Sci. Engrg.》、《J. Math. Anal. Appl.》等SCI学术期刊上发表学术论文20余篇。主持多项国家自然科学基金和河北省自然科学基金。2015年至2016年于加拿大西安大略大学访学。

报告题目4：Physical measures for a class of partially hyperbolic attractors

报告人：曹永罗教授，苏州大学

报告时间：2023年10月26日8:00-9:00

报告地点：20-404

报告摘要：In this talk, we consider the existence of SRB measure for partially hyperbolic attractors. If the systems's central direction can be decomposed into one dimension sub-bundles which are dominated splitting, and all u-gibbs measures are hyperbolic, then there exist finite physical measures.

报告人简介：曹永罗，苏州大学教授、数学科学学院院长、博士生导师，主要从事微分动力系统遍历理论以及动力系统维数理论的研究。2013年获江苏省教学成果奖一等奖，主持国家自然科学基金重大项目以及多项国家自然科学基金和973项目基金。在GAFA、CMP、Trans. AMS.、Math.Z、ETDS、JDE、JFA、Nonlinearity等国际权威期刊上发表论文60余篇，目前担任期刊Dynamical Systems编委。

报告题目5：The limit cycles for a class of non-autonomous piecewise differential equations

报告人：赵育林教授，中山大学数学学院（珠海）

报告时间：2023年10月26日9:00-10:00

报告地点：20-404

报告摘要：This paper studies a class of non-autonomous piecewise differential equations defined by 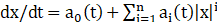, where n ∈ N+ and a_i(t) are real, 1-periodic and smooth functions. We deal with two basic problems with its limit cycles (isolated solutions satisfying x(0) = x(1)). First, we give a proof that there is no upper bound for the number of limit cycles of the above type equations for any n ∈ N⁺. Second, we demonstrates that if a₁(t), · · · , a_n(t) do not change sign and have the same sign in the interval [0, 1], then the equation has at most two limit cycles. Furthermore, we analyze all possible configurations of these limit cycles. Additionally, we extend the result of at most two limit cycles to a broader class of general non-autonomous piecewise polynomial differential equations and provide a criterion for determining the uniqueness of the limit cycle within this class of equations.

报告人简介：赵育林，中山大学数学学院（珠海）教授、博士生导师，广东省本科高校教学指导委员会数学专业委会委员，广东省数学会常务理事。主要从事常微分方程定性理论和分支理论的研究工作，包括弱化的Hilbert 16问题、周期单调性、代数极限环、高阶极限环分支问题等。近年来，赵育林教授一直从事向量场分支理论和周期单调性的研究工作，已在J. Differential Equation、Nonlinearity、中国科学(英文版)等杂志发表文章70余篇。先后主持国家自然科学基金6项、教育部博士点学科基金一项、教育部留学回国人员启动基金一项。获2019年度广东省自然科学奖二等奖。

报告题目6：Melnikov analysis for a integrable system

报告人：于江教授，上海交通大学

报告时间：2023年10月26日10:00-11:00

报告地点：20-404

报告摘要：This talk introduces a completed Melnikov analysis of any order for a class of perturbed integrable non-Hamiltonian system. The exact upper bounds of the number of limit cycles bifurcated from the period annulus are obtained by analysing the algebraic structures from explicit expressions of any order Melnikov functions.

报告人简介：于江，上海交通大学数学科学学院长聘教授，博士生导师。1999年于北京大学获博士学位。从事微分方程定性和分岔理论研究。主持并参与多项国家自然科学基金面上和重点项目，在Communications in Mathematical Physics、Journal of Differential Equations、Nonlinearity、Journal of Geometry and Physics等国际重要学术期刊上发表了一系列高水平学术论文。

报告题目7：Bifurcation of limit cycles near homoclinic loops in near-Hamiltonian systems by Picard-Fuchs equations

报告人：田云教授，上海师范大学

报告时间：2023年10月26日11:00-12:00

报告地点：20-404

报告摘要：In this talk, we consider the bifurcation of limit cycles near a homoclinic loop in planar near-Hamiltonian systems by high-order Melnikov functions. We present a method combining the algebraic structure of Abelian integrals and Picard-Fuchs equation for computing the corresponding asymptotic expansion of Melnikov functions near the loop. For cubic perturbations of a cubic cuspidal loop, using this method we show that planar cubic systems can have ten limit cycles bifurcating near a homoclinic loop. This method can be extended to the case of heteroclinic loops.

报告人简介：田云，加拿大西安大略大学应用数学博士，现为上海师范大学数理学院教授，博士生导师，主要从事微分方程定性理论、计算机符号计算和传染病模型等方向的研究，特别关注弱化的Hilbert第16问题、同宿异宿极限环分支和规范型的符号计算等相关问题。近年来，在JDE、Commun. Nonl. Sci. Numer. Simul和Nonlinear Anal. RWA等本领域主流期刊发表学术论文三十余篇。主持国家自然科学基金项目两项。

报告题目8：弱KAM理论最新进展

报告人：王楷植教授，上海交通大学

报告时间：2023年10月26日14:00-15:00

报告地点：20-404

报告摘要：首先简要介绍哈密顿系统弱KAM理论的经典结果。然后，介绍时间周期哈密顿系统、切触哈密顿系统弱KAM理论的最新进展，以及弱KAM方法在平均场博弈系统研究中的具体应用。报告内容基于报告人与几位学者合作的工作。

报告人简介：王楷植，上海交通大学数学科学学院教授、博导、院长助理，上海高校特聘教授(东方学者)。主要从事弱KAM理论及其应用方面的研究，在《Communications in Mathematical Physics》，《Journal de Mathématiques Pures et Appliquées》，《SIAM Journal on Mathematical Analysis》，《SIAM Journal on Applied Dynamical Systems》，《Communications in Partial Differential Equations》等学术杂志上发表多篇论文。主持包括国家自然科学基金面上项目、国家自然科学基金青年基金项目、教育部博士点基金和中国博士后基金项目在内的多项科研项目。

报告题目9：Unfolding and bifurcation of some planar degenerate differential systems

报告人：唐异垒教授，上海交通大学

报告时间：2023年10月26日15:00-16:00

报告地点：20-404

报告摘要：In this talk we introduce bifurcations and unfolding of some planar systems at degenerate equilibria and display their all bifurcations.

报告人简介：唐异垒，上海交通大学数学科学学院教授，主要从事微分方程和动力系统的定性理论与分支理论的研究，包括退化系统的分岔和开折、连续与不连续微分系统的全局动力学和分岔等。先后到英国、西班牙、意大利、匈牙利等国访问。主持过国家自然科学基金和国家重点子课题；2016年获得欧盟玛丽-居里学者基金；2018年获得科技部国际合作项目资助；两次获得上海交通大学晨星青年学者等基金资助。研究结果发表在J. Differential Equations、Nonlinearity、Physica D、SIAM J. Appl. Math. 等期刊。

报告题目10：Dynamics of the classical predator-prey model with the generalized Holling III functional response

报告人：张祥教授，上海交通大学

报告时间：2023年10月27日9:30-10:30

报告地点：20-404

报告摘要：In this talk we introduce our recent results on the global dynamics of the classical predator-prey models with the generalized Holling type III functional response. We will show that this system has rich dynamics, such as sub-and supercritical Hopf bifurcation, Bogdanov-Takens bifurcation, relaxation oscillation, canard explosion, homoclinic and heteroclinic connections and so on. Some of them are new found phenomena. The main tools are qualitative and bifurcation theories together with singular perturbation theory.

报告人简介：张祥，上海交通大学特聘教授。从事动力系统的定性、分支和可积理论，以及奇异摄动理论的研究。曾在美国佐治亚理工学院和西班牙巴塞罗那数学研究中心任访问教授。主要结果发表在American J. Math.、Comm. Math Phys.、J. Differential Equations、 J. Functional Analysis、Trans. Amer. Math. Soc. 等国际期刊上。目前担任中国数学会奇异摄动专业委员会主任、以及IJBC和QTDS等SCI杂志的编委等。