报告题目1：A restricted memory quasi-Newton bundle method for nonsmooth optimization on Riemannian manifolds

报告人：唐春明

报告时间：2022年12月9日（周五）上午11:00-12:00

腾讯会议ID：570 918 934

摘要：In this talk, a restricted memory quasi-Newton bundle method for minimizing a locally Lipschitz function over a Riemannian manifold is proposed, which extends the classical ones in Euclidean space to the manifold setting. The potential second order information of the objective function is approximated by applying the Riemannian versions of the quasi-Newton updating formulas. The subgradient aggregation technique is used to avoid solving the time-consuming quadratic programming subproblem when calculating the candidate descent direction.  Moreover, a new Riemannian line search procedure is proposed to generate the stepsizes. Global convergence of the proposed method is established: if the serious iteration steps are finite, then the last serious iteration is stationary; otherwise every accumulation point of the serious iteration sequence is stationary. Finally, some preliminary numerical results show that the proposed method is promising.

报告人简介：唐春明，广西大学数学与信息科学学院教授，博士，博士生导师，广西运筹学会副理事长，中国运筹学会理事，广西数学会常务理事。1998-2004年本、硕就读于广西大学，2008年博士毕业于上海大学，2014年到澳大利亚新南威尔士大学访学一年。目前主要研究非光滑优化算法。主持国家自然科学基金项目4项，广西自然科学基金项目3项。在《 European Journal of Operational Research》《Journal of Optimization Theory and Applications》《Computational Optimization and Applications》《Optimization Letters》《Optimization》《Numerical Algorithms》《IEEE Transactions on Power Systems》《中国科学：数学》等重要刊物发表论文40余篇。

报告题目2：A stochastic linearized proximal method of multipliers for convex stochastic optimization with expectation constraints

报告人：张立卫

报告时间：2022年12月9日（周五）下午14:00-15:00

腾讯会议ID：593 667 909

摘要：This talk considers the problem of minimizing a convex expectation function with a set of inequality convex expectation constraints. We present a computable stochastic approximation type algorithm, namely the stochastic linearized proximal method of multipliers, to solve this convex stochastic optimization problem. This algorithm can be roughly viewed as a hybrid of stochastic approximation and the traditional proximal method of multipliers. Under mild conditions, we show that this algorithm exhibits 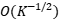 expected convergence rates for both objective reduction and constraint violation if parameters in the algorithm are properly chosen, where K denotes the number of iterations. Moreover, we show that, with high probability, the algorithm has  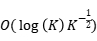      ) constraint violation bound and  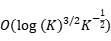objective bound. Some preliminary numerical results demonstrate the performance of the proposed algorithm.

报告人简介：张立卫教授，大连理工大学数学科学学院运筹学与控制论业博士生指导教师，金融数学与保险精算专业博士生指导教师。他于1989年，1992年，1998年分别在大连理工大学获得理学学士，硕士，博士学位，1999-2001在中科院计算数学所从事博士后工作。目前的研究兴趣是“矩阵优化”，“随机规划”与“均衡优化”。他完成和主持自然科学基金面上基金多项,重点基金子课题两项。在国际顶级期刊Mathematical  Programming, Operations Research,  SIAM Journal on Optimization, Mathematics of Operations Research,  INFORMS Journal on Computing, Mathematics of Computation 发表论文10多篇。现任中国运筹学会常务理事，中国运筹学会数学规划分会副理事长，中国运筹学会金融工程与金融风险管理分会副理事长,《JAPOR》和《运筹学学报》编委，2020年获得中国运筹学会运筹研究奖。

邀请人：张莹